【学习笔记】多项式基础

FFT

多项式的加法，减法显然有 $O(n)$ 的做法，而计算多项式乘法则需要 $O(n^2)$ 的时间，我们需要一些更快的做法。

我们有一个结论：

$n+1$ 个不同的点可以唯一确定一个 $n$ 次多项式。

一个 $n$ 次多项式 $F(x)$ 就可以被写作

$$\{(x_0,F(x_0)),(x_1,F(x_1)),\ldots, (x_n,F(x_n)\} \nonumber$$

这被称作多项式的点值表示，而原来的表示法被称为多项式的系数表示。

证明：

假设 $F(x)=p_0+p_1x^1+p_2x^2+\ldots + p_nx^n$

那么我们把 $n+1$ 个不同的 $x$ 代入，我们可以得到一个线性方程组：

$$\left\{\begin{aligned} F(x_0)&=p_0+p_1x_0+p_2x_0^2+\ldots+p_nx_0^n\\ F(x_1)&=p_0+p_1x_1+p_2x_1^2+\ldots+p_nx_1^n\\ F(x_2)&=p_0+p_1x_2+p_2x_2^2+\ldots+p_nx_2^n\\ &\cdots\\ F(x_n)&=p_0+p_1x_n+p_2x_n^2+\ldots+p_nx_n^n\\ \end{aligned}\right. \nonumber$$

这可以被写成矩阵的形式：

$$\begin{bmatrix} F(x_0)\\ F(x_1)\\ F(x_2)\\ \vdots\\ F(x_n)\\ \end{bmatrix} = \begin{bmatrix} 1 &x_0 &x_0^2 &\cdots &x_0^n\\ 1 &x_1 &x_1^2 &\cdots &x_1^n\\ 1 &x_2 &x_2^2 &\cdots &x_2^n\\ \vdots &\vdots &\vdots &\ddots &\vdots\\ 1 &x_n &x_n^2 &\cdots &x_n^n\\ \end{bmatrix} \begin{bmatrix} p_0\\ p_1\\ p_2\\ \vdots\\ p_n \end{bmatrix} \nonumber$$

中间的是范德蒙德矩阵，由于我们选的 $n+1$ 个 $x$ 两两不同，则其行列式不为 $0$，线性方程组有唯一解。

那么对于两个 $n$ 次多项式，我们求出他们在 $2n+1$ 个不同的 $x$ 时的取值，然后把对应位置的值相乘，然后再还原为系数表示，我们就知道了两个多项式相乘的结果，中间相乘的过程是 $O(n)$ 的。

唯一的问题是，我们怎么在低于 $O(n^2)$ 的时间内求出系数表示的点值表示/把点值表示还原为系数表示？

我们最大的突破口在于可以随意选取初值，让我们尝试借助这个特性来加速求解。

为了方便，接下来我们设所要操作的多项式都是 $2^k-1$ 次的，如果不足，可以在高次项补 $0$。

DFT

大致流程

一个关键的想法是，如果 $f(x)$ 是一个偶函数，那么 $f(x)=f(-x)$，所以我们只要计算一个点的点值就知道了两个点的点值。

如果 $f(x)$ 是个奇函数，则 $f(x)=-f(-x)$，仍然是计算一个值即可。

那么我们不妨把 $F$ 分为奇偶两部分，即：

$$\begin{aligned} F(x)&=a_0+a_1x+a_2x^2+\cdots + a_nx^n\\ &=(a_0+a_2x^2+\cdots)+x(a_1+a_3x^2+\cdots)\\ &=F_e(x^2)+xF_o(x^2) \end{aligned} \nonumber$$

那么

$$\begin{aligned} F(x_i)&=F_e(x^2)+xF_o(x^2)\\ F(-x_i)&=F_e(x^2)-xF_o(x^2) \end{aligned} \nonumber$$

再对 $F_e(x^2)$ 与 $F_o(x^2)$ 递归计算即可。

由于我们初始选取的所有点对都是相反数，那么递推的时候就只剩下 $\frac{n}{2}$ 个点。如此递归计算，复杂度即为 $O(n\log n)$。

但是不难注意到一个问题，我们在递归子问题时，实际上代入的是 $x^2$ 而不是 $x$，那么我们就没有办法取相反数，因为在实数域内，$x^2$ 总应该是正数。

让我们举一个例子看看上述过程是怎么做的，从而考察我们所选的数需要有什么性质。假设我们要将一个三次多项式 $F(x)=-1-2x+x^2+x^3$ 转为点值表示，为此我们需要求其在四个点 $x_0,-x_0,x_1,-x_1$ 的值，那么首先拆成：

$$\begin{aligned} F_e(x^2)&=-1+x^2\\ F_o(x^2)&=-2+x^2\\ F(x)&=F_e(x^2)+xF_o(x^2)\\ \end{aligned} \nonumber$$

那么，求出 $F_e(x_0^2)$ 与 $F_o(x_0^2)$ 的值，就可以直接推出

$$\begin{aligned} F(x_0)&=F_e(x_0^2)+x_0F_o(x_0^2)\\ F(-x_0)&=F_e(x_0^2)-x_0F_o(x_0^2)\\ \end{aligned} \nonumber$$

而 $x_1$ 的情况类似。

$$\begin{aligned} F(x_1)&=F_e(x_1^2)+x_1F_o(x_1^2)\\ F(-x_1)&=F_e(x_1^2)-x_1F_o(x_1^2)\\ \end{aligned} \nonumber$$

接下来，我们要求 $F_e(x)$ 在 $x_0^2$ 与 $x_1^2$ 处的值，并且现在 $x_1^2=-x_0^2$，我们先不管这是怎么做到的。记 $F_e$ 为 $G$。

再次类似地拆开：

$$\begin{aligned} G_e(x^4)&=-1\\ G_o(x^4)&=1\\ G(x^2)&=G_e(x^4)+x^2G_o(x^4) \end{aligned} \nonumber$$

因为 $x_1^2=-x_0^2$，且我们直接知道 $G_e(x^4)$ 与 $G_o(x^4)$ 就是常数，所以立刻有：

$$\begin{aligned} G(x_0^2)=G_e(x^4)+x_0^2G_o(x^4)=-1+x_0^2\\ G(x_1^2)=G_e(x^4)-x_0^2G_o(x^4)=-1-x_0^2 \end{aligned} \nonumber$$

并且，$F_o$ 的情况也类似，再回退即可递推完。

总结一下，我们需要的一组 $x$ 需要满足的性质是：

1. $x_0,x_1,x_2,\cdots,x_{2^k-1}$，其中 $x_0,x_{2^{k-1}}$ 互为相反数，$x_1,x_{2^{k-1}+1}$ 互为相反数……（这里的顺序与上面略有不同，为了实现方便与适配下面的内容）
2. 令每个数都变为其平方，此时 $x_0^2=x_{2^{k-1}}^2$，$x_1^2=x_{2^{k-1}+1}^2$……，我们去掉所有重复的数，变为 $x_0^2,x_1^2,x_3^2,\cdots, x_{2^{k-1}-1}^2$，此时如果把他们重新标定为 $x_0',x_1',\cdots, x_{2^{k-1}-1}'$，它们仍满足 $1$ 中的条件，并且每次重复 $2$ 直到序列中仅剩一个数，它们都满足 $1$ 的条件。

实数域显然没有办法达成上述条件，考虑令 $x$ 为复数。

单位根

在复数域中，一些满足我们需求的数是单位根，并且可以证明，这是唯一满足我们需求的数。

以下的 $n$ 指的是我们所需的多项式的项数，即次数$+1$，这意味着 $n$ 是一个 $2$ 的幂。

以单位圆点为起点，单位圆的 $n$ 等分点为终点，我们可以得到 $n$ 个复数。我们称 $n$ 次本原单位根是它们之中幅角为正且最小的复数，也就是：

$$\omega_n=\cos\frac{2\pi}{n}+i\sin\frac{2\pi}{n} \nonumber$$

根据欧拉公式，我们将 $\omega_n$ 写作 $e^{i\frac{2\pi}{n}}$（或者直接从复数乘法就是旋转的角度）可以知道：

$$\begin{aligned} \omega_n^k=\cos\frac{2k\pi}{n}+i\sin\frac{2k\pi}{n} \end{aligned} \nonumber$$

仔细观察可以发现几条非常好的性质：

1. $\omega_n^{k+\frac{n}{2}}=-\omega_n^k,k\in \mathbb N^+$

   这条性质我们把前面的式子展开成 $\omega^{k}_n\omega_n^{\frac{n}{2}}$，再把后面的代入上式即可证明。

   这意味着我们如果把初始的 $x_0,x_1,x_2,\cdots, x_n$ 选为 $\omega_n^{0},\omega_n^{1},\omega_n^{2},\cdots, \omega_n^{n-1}$

   那么这就满足上面所需的第一条要求，$\omega_n^0$ 与 $\omega_n^{\frac{n}{2}}$ 是一组，$\omega_n^1$ 与 $\omega_n^{1+\frac{n}{2}}$ 是一组……每组中均互为对方的相反数。

2. $\omega_{kn}^{kr}=\omega_{n}^{r},r\in \mathbb N^{+}$

   这条性质仍然是直接展开即得证。

   现在我们将所有数逐个平方，即变为 $\omega_n^{0},\omega_n^{2},\omega_n^{4},\cdots, \omega^{2n-2}_n$，由于去重的原因后半部分不用管，只留 $\omega_n^{0},\omega_{n}^2,\omega_n^{4},\cdots,\omega_{n}^{n-2}$。

   由这条性质，我们可以把上面的再写成：

   $$\omega_{\frac{n}{2}}^{0},\omega_{\frac{n}{2}}^{1},\omega_{\frac{n}{2}}^{2},\cdots,\omega_{\frac{n}{2}}^{\frac{n}{2}-1} \nonumber$$

   这又恰好满足了我们上面所需性质 $2$ 中重新标定的需求！并且这一组单位根只是把 $n$ 缩小到原来的 $\frac{1}{2}$，自然仍然满足性质 $1$，单位根的性质完美契合了我们的所需！

实现

至此我们已经可以写出将多项式的系数表示转化为点值表示的过程，只要我们将我们需要求的 $x$ 选为 $n$ 次单位根的各次幂即可，给出一份最朴素的实现：

//a数组最开始是系数表示
void FFT(std::complex<double> *a, int n) {
    //当递归到序列长度为 1 时, n 次单位根变为原来的 n 次方, 也就是 1, 所以这个时候的值直接就是对应位置的系数
	if(n == 1)
		return ;
	int mid = n >> 1;
    //奇偶分组, 暂存下此时的系数
	std::complex<double> A1[mid + 1], A2[mid + 1];

	for(int i = 0; i <= n; i += 2) {
		A1[i >> 1] = a[i];
		A2[i >> 1] = a[i + 1];
	}
	FFT(A1, mid);
	FFT(A2, mid);
	
    //此时A1, A2已经是 n / 2 个点的系数表示
    //wn 是 n 次单位根
	std::complex<double> w0(1, 0), wn(cos(2 * pi / n), sin(2 * pi / n));
    //求 x 为 w_n^0, w_n^1, w_n^1, ..., w_n^{n-1} 时分别的解
	for(int i = 0; i < mid; i++, w0 *= wn) {
        //F(x) = F_e(x) + x * F_o(x)
		a[i] = A1[i] + w0 * A2[i];
        //F(-x) = F_e(x) - x * F_o(x)
		a[i + (n >> 1)] = A1[i] - w0 * A2[i];
	}
}

IDFT

我们还得把点值表示换成系数表示，所幸这部分其实非常的简单，与 FFT 几乎完全相同。

先不管上面的 FFT 干了啥，考虑暴力的系数表示转点值表示。

$$\left\{\begin{aligned} F(\omega_n^0)&=a_0+a_1(\omega_n^0)^1+a_2\omega(\omega_n^0)^2+\cdots+a_{n-1}(\omega_n^0)^{n-1}\\ F(\omega_n^1)&=a_0+a_1(\omega_n^1)^1+a_2\omega(\omega_n^1)^2+\cdots+a_{n-1}(\omega_n^1)^{n-1}\\ &\cdots\\ F(\omega_n^{n-1})&=a_0+a_1(\omega_n^{n-1})^1+a_2\omega(\omega_n^{n-1})^2+\cdots+a_{n-1}(\omega_n^{n-1})^{n-1}\\ \end{aligned}\right. \nonumber$$

这可以被写成一个线性变换的形式：

$$\begin{bmatrix} F(\omega_{n}^{0})\\ F(\omega_{n}^{1})\\ F(\omega_{n}^{2})\\ \vdots\\ F(\omega_n^{n-1}) \end{bmatrix} = \begin{bmatrix} 1 &(\omega_n^0)^1 &(\omega_n^0)^2 &\cdots &(\omega_n^0)^{n-1}\\ 1 &(\omega_n^1)^1 &(\omega_n^1)^2 &\cdots &(\omega_n^1)^{n-1}\\ 1 &(\omega_n^2)^1 &(\omega_n^2)^2 &\cdots &(\omega_n^2)^{n-1}\\ \vdots &\vdots &\vdots &\ddots &\vdots\\ 1 &(\omega_n^{n-1})^1 &(\omega_n^{n-1})^2 &\cdots &(\omega_n^{n-1})^{n-1}\\ \end{bmatrix} \begin{bmatrix} a_0\\ a_1\\ a_2\\ \cdots\\ a_{n-1} \end{bmatrix} \nonumber$$

FFT 实际上就是算了上面的这样一个矩阵乘法。

所以我们只要在左边的系数表示左乘中间的范德蒙德矩阵的逆矩阵，就得到了系数表示。

中间的矩阵形式非常好，直接给出结论：其逆矩阵就是每个元素先取倒数，再除以变换长度 $n$。

为啥直接给出结论是因为我不想算了

而如果我们要将单位根取倒数，这实际上就是：

$$\omega_n^{-1}=e^{-i\frac{2\pi}{n}}=\cos-\frac{2\pi}{n}+i\sin-\frac{2\pi}{n}=\cos\frac{2\pi}{n}-i\sin\frac{2\pi}{n} \nonumber$$

所以我们在 FFT 的过程中将所有单位根虚部取成相反数，所得到的就是 IDFT 的过程，至于除以 $n$，可以在计算完成后一并解决。

//inv = 1 时为 FFT, inv = -1 时为 IDFT
void FFT(std::complex<double> *a, int n, int inv) {
	if(n == 1)
		return ;
	int mid = n >> 1;
	std::complex<double> A1[mid + 1], A2[mid + 1];

	for(int i = 0; i <= n; i += 2) {
		A1[i >> 1] = a[i];
		A2[i >> 1] = a[i + 1];
	}
	FFT(A1, mid, inv);
	FFT(A2, mid, inv);
	
    //虚部乘上相反数
	std::complex<double> w0(1, 0), wn(cos(2 * pi / n), inv * sin(2 * pi / n));
	for(int i = 0; i < mid; i++, w0 *= wn) {
		a[i] = A1[i] + w0 * A2[i];
		a[i + (n >> 1)] = A1[i] - w0 * A2[i];
	}
}

DFT & IDFT 的完整实现

完整的模板题代码是：

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <complex>
#include <cmath>

const int maxn = 1 << 22;
const double eps = 1e-6, pi = acos(-1.0);

std::complex<double> a[maxn], b[maxn];
int n, m;

void FFT(std::complex<double> *a, int n, int inv) {
	if(n == 1)
		return ;
	int mid = n >> 1;
	std::complex<double> A1[mid + 1], A2[mid + 1];

	for(int i = 0; i <= n; i += 2) {
		A1[i >> 1] = a[i];
		A2[i >> 1] = a[i + 1];
	}
	FFT(A1, mid, inv);
	FFT(A2, mid, inv);

	std::complex<double> w0(1, 0), wn(cos(2 * pi / n), inv * sin(2 * pi / n));
	for(int i = 0; i < mid; i++, w0 *= wn) {
		a[i] = A1[i] + w0 * A2[i];
		a[i + (n >> 1)] = A1[i] - w0 * A2[i];
	}
}

int main(){
	scanf("%d%d", &n, &m);
	for(int i = 0; i <= n; i++) {
		double x;
		scanf("%lf", &x);
		a[i].real(x);
	}

	for(int i = 0; i <= m; i++) {
		double x;
		scanf("%lf", &x);
		b[i].real(x);
	}
	
	int len = 1 << std::max((int)ceil(log2(n+m)), 1);
	FFT(a, len, 1);
	FFT(b, len, 1);
	for(int i = 0; i <= len; i++)
		a[i] = a[i] * b[i];
	
	FFT(a, len, -1);
	for(int i = 0; i <= n + m; i++)
		printf("%.0f ", a[i].real() / len + eps);
	puts("");
	return 0;
}

NTT

大量的浮点运算会带来精度误差，也会大大减缓效率，可惜在复数域 $\mathbb C$ 中单位根是我们唯一满足需求的数，但我们大多数的多项式题中，运算实际上在 $\mathbb Z/p\mathbb Z$ 中进行，而 $p$ 通常是一个素数。我们希望我们所有的运算都在模意义下完成，所幸在这种情况下，FFT 有一个替代品，我们称之为 NTT，即快速数论变换。

所有复数运算都产生自单位根，如果我们希望不使用复数进行计算，就需要找到单位根的替代品。考虑我们需要单位根的哪些性质：

1. $\omega_n^{k+\frac{n}{2}}=-\omega_n^k,k\in \mathbb N^+$
2. $\omega_{kn}^{kr}=\omega_{n}^{r},r\in \mathbb N^{+}$
3. $\omega_n^{-1}=\cos\frac{2\pi}{n}-i\sin\frac{2\pi}{n}$

最后一条性质是无关紧要的，我们求逆即可。

如果了解过原根的性质，我们会发现其在模 $p$ 意义下和我们要求的东西相当接近。

不了解原根也没关系，下面简单介绍一下它在 NTT 中应用的性质：

原根与阶

如果正整数 $a$ 与正整数 $p$ 互质，并且 $p>1$，那么对于满足 $a^n\equiv 1\pmod p$ 的最小的 $n$，我们称其为 $a$ 模 $p$ 的阶，记作 $\delta_p(a)$。

阶最重要的性质是，对于所有的 $i\in [0,\delta_p(a))$，所有 $a^i\bmod p$ 的结果两两不同。

我们反证，假设 $k,j\in [0,\delta_p(a))$ 满足 $a^k\equiv a^j\pmod p$，那么 $a^{k-j}\equiv 1\pmod p$，与定义矛盾。

而如果 $g$ 与 $n$ 满足 $\delta_n(g)=\varphi(n)$，且 $\gcd(g,n)=1$，则 $g$ 为 $n$ 的一个原根。

如果 $\gcd(g,n)=1$ 且 $n>0$，那么 $g$ 为 $n$ 的一个充要条件是 $\{g^1,g^2,g^3,\cdots, g^{\varphi(n)}\}$ 是 $n$ 的一组简化剩余系。这是因为由阶的定义，集合中的任意两个元素模 $n$ 不同余，且 $\gcd(g,n)=1$，则该集合就是 $n$ 的一组简化剩余系。

说了这么多定义，原根到底为什么满足我们上面的要求？

通常模数都是素数，那么 $\varphi(p)=p-1$，所以 $p$ 的一个原根 $g$ 自然满足 $\gcd(p,n)=1$，则 $g$ 的从 $1$ 到 $p-1$ 次方在模 $p$ 意义下可以取遍 $1\sim p-1$ 中的每一个值。并且每个值唯一对应一个 $g^k,k\in[1,p-1)$

现在我们假设 $n | (p-1)$，$n$ 与上面意义相同，都是 $2$ 的某个幂，定义

$$g_n=g^{\frac{p-1}{n}} \nonumber$$

根据费马小定理，我们有 $g_n^n=g^{n\frac{p-1}{n}}=g^{p-1}=1$，也就是这仍然是每 $n$ 次方一循环的，与单位根相同。

单位根的性质 $1$，$\omega_n^{k+\frac{n}{2}}=-\omega_n^k,k\in \mathbb N^+$ 可以被等价地叙述为 $\omega_n^{\frac{n}{2}}=-\omega_n$

让我们考虑 $g_n^{\frac{n}{2}}$：

$$\begin{aligned} g^{\frac{n}{2}}_{n}&=g^{\frac{n}{2}\cdot\frac{p-1}{n}}\\ &=g^{\frac{p-1}{2}} \end{aligned} \nonumber$$

又因为

$$(g^{\frac{p-1}{2}})^2=g^{p-1},g^{p-1}\equiv 1\pmod p \nonumber$$

根据原根的定义，$g^{\frac{p-1}{2}}$ 必定不与 $1$ 同余，因为如果这样就不满足每一个值唯一对应一个 $g^k,k\in[1,p-1)$

所以就一定有：

$$g_n^{\frac{n}{2}}\equiv -1\pmod p \nonumber$$

满足我们所需的性质 $1$。

对于满足性质 $2$ 的证明是简单的：

$$\begin{aligned} g^{rk}_{rn}=g^{\frac{rk(p-1)}{rn}}=g^{k}_n \end{aligned} \nonumber$$

所以如果我们直接把上面 FFT 的代码中的单位根全部替换成对应的 $g_n$，就可以得到 NTT 的代码了。

唯一的问题是，我们总是需要满足 $n|p-1$，而我们常用的模数 $998244353$ 满足 $998244352=7\times17\times2^{23}$，而 $1004535809$ 满足 $1004535808=479\times 2^{21}$，$469762049$ 满足 $469762048=7\times 2^{26}$，可惜的是 $1000000007$ 的性质就要差得多，$1000000006=2\times 500000003$，对于这种情况，我们将在后面介绍解决方法。

到这里我们就可以写出 NTT 了，但这个多项式乘法也太慢了，能不能更猛一点啊？

优化

位逆序置换 / 蝴蝶变换

上面的实现中，我们每次递归都要申请两个长度为 $mid$ 空间，做一遍分拆系数……

最大的问题在于我们要分拆系数赋值，如果我们从一开始就把每个系数放到目标位置上，那么我们就直接两个两个合并，四个四个合并……每次倍增即可完成整个过程。

考虑我们是怎么把每个系数 $a_i$ 放到目标位置上的。

从低到高逐位考虑 $i$ 二进制的每一位，如果是 $1$ 我们就把他放在序列右半边，递归右边，如果是 $0$ 就放到序列左半边，递归左半边。

不难想到这样逐步进行下去，递归到底时其位置就是 $i$ 的二进制翻转

那么我们直接把每个系数要放到的位置处理出来，然后两两合并就可以了，省去了中间大量的申请内存与复制的时间。

而目标要换到的位置实际上是可以线性预处理出来的，假设 $\operatorname{rev}(i)$ 表示下标为 $i$ 的系数最终要移动到的位置。

从小到大做，而 $\operatorname{rev}(0)=0$

那么我们已经知道了 $\operatorname{rev}(\lfloor\frac{i}{2}\rfloor)$ 的结果。我们要翻转 $i$，可以看做先翻转 $\lfloor\frac{i}{2}\rfloor$，将其右移一位，然后再最高位上填上末尾。

举个例子，我们要翻转 $\color{red}{01101010}\color{green}1$，我们已经知道了 $0\color{red}01101010$(先去掉末位再在前面补 $0$)，那么翻转之后就是 $\color{red}{01010110}\color{black}{0}$，去掉最后一位变成 $\color{red}{01010110}$，随后在最前面补上 $1$，就变成 $\color{green}1\color{red}{01101010}$，这就是我们所需的翻转。

假设整个序列的长度是 $2^k$，那么：

$$\operatorname{rev}(i)=\left\lfloor\frac{\operatorname{rev}(\lfloor\frac{i}{2}\rfloor)}{2}\right\rfloor+(i\bmod 2)\times 2^{k-1} \nonumber$$

接下来考虑怎么合并答案。

现在假设我们已经有了 $F_e(\omega_{n/2}^{k})$ 和 $F_o(\omega^{k}_{n/2})$ 的答案，那么他们分别存在数组里 $k$ 与 $k+\frac{n}{2}$ 的位置，而我们借助这两个值算出来的 $F(\omega_n^{k})$ 与 $F(\omega^{k+\frac{n}{2}}_n)$ 恰好放在同样的位置，直接覆盖即可。

具体实现可以看代码：

int k = std::max((int)ceil(log2(n+m)), 1);
int len = 1 << k;
//预处理rev
for(int i = 0; i < len; i++)
	rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (k - 1));

void NTT(ll *a, int n, int inv){
    //将系数换到置换对应的位置
	for(int i = 0; i < n; i++)
		if(i < rev[i])
			std::swap(a[i], a[rev[i]]);
	
    //变换的区间长度
	for(int i = 1; i < n; i <<= 1) {
        //这部分可以预处理单位根做到更快
		ll gn = f_pow(inv ? g : gi, (mod - 1) / (i << 1));

		for(int j = 0; j < n; j += (i << 1)) {
			ll g0 = 1;
			for(int k = 0; k < i; k++, g0 = g0 * gn % mod) {
                //直接覆盖原来的值
				ll x = a[j + k], y = g0 * a[i + j + k] % mod;
				a[j + k] = (x + y) % mod;
				a[i + j + k] = (x - y + mod) % mod;
			}
		}
	}
}

这还可以通过减少取模次数进一步优化。

能不能再猛一点啊？

上面的 NTT 再加上预处理单位根与逆元就已经足够应付大多数的情况，下面的内容可以暂时略过。

参考资料：

yhx-12243 的 NTT 到底写了些什么（详细揭秘） - Seniorious’ blog

转置原理及其应用

完整多项式模板 (yhx-12243.github.io)

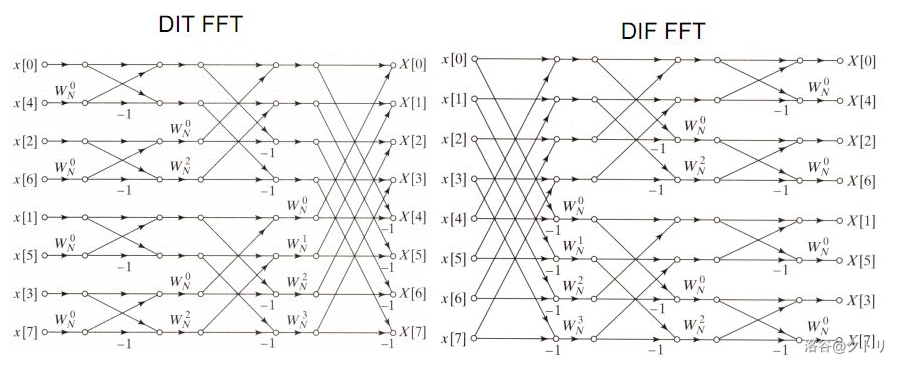
DIF-FFT

上面的每次按奇偶划分的做法被称为DIT(按时域抽取)-FFT，其作用可以概括为输入一个经过蝴蝶变换后的系数向量，输出一个点值向量

而DIF(按频域抽取)-FFT是其转置，作用是输入一个系数向量，输出一个蝴蝶变换后的点值向量

太抽象了，先不管这玩意是啥意思，我们考虑换一个角度做 FFT，现在我们已经知道 FFT 的取值都是单位根了，我们从单位根下手：

假设我们要求 $F(\omega_n^k)$

$$\begin{aligned} F(\omega_n^{k}) &=\sum_{i=0}^{n-1}a_i\omega_n^{ki}\\ &=\sum_{i=0}^{\frac{n}{2}-1}a_i\omega_n^{ki}+\sum_{i=\frac{n}{2}}^{n-1}a_i\omega_n^{ki}\\ &=\sum_{i=0}^{\frac{n}{2}-1}a_i\omega_n^{ki}+\sum_{i=0}^{\frac{n}{2}-1}a_{i+\frac{n}{2}}\omega_n^{k(\frac{n}{2}+i)}\\ &=\sum_{i=0}^{\frac{n}{2}-1}a_i\omega_n^{ki}+\sum_{i=0}^{\frac{n}{2}-1}a_{i+\frac{n}{2}}\omega_n^{\frac{kn}{2}+ki}\\ &=\sum_{i=0}^{\frac{n}{2}-1}a_i\omega_n^{ki}+\sum_{i=0}^{\frac{n}{2}-1}a_{i+\frac{n}{2}}\omega_n^{\frac{kn}{2}+ki}\\ &=\sum_{i=0}^{\frac{n}{2}-1}\bigg(a_i+a_{i+\frac{n}{2}}\omega_n^{\frac{kn}{2}}\bigg)\omega_n^{ki}\\ &=\sum_{i=0}^{\frac{n}{2}-1}\bigg(a_i+(-1)^ka_{i+\frac{n}{2}}\bigg)\omega_n^{ki}\\ &=\sum_{i=0}^{\frac{n}{2}-1}a_i\omega^{ki}+\sum_{i=0}^{\frac{n}{2}-1}(-1)^ka_{i+\frac{n}{2}}\omega_n^{ki} \end{aligned} \nonumber$$

按 $k$ 的奇偶性分类讨论，如果我们的 $k$ 是一个偶数，那么

$$F(\omega_n^{k})=(\sum_{i=0}^{\frac{n}{2}-1}a_i+\sum_{i=0}^{\frac{n}{2}-1}a_{i+\frac{n}{2}})\omega_n^{ki} \nonumber$$

如果我们的 $k$ 是一个奇数，那

$$F(\omega_n^k)=(\sum_{i=0}^{\frac{n}{2}-1}a_i-\sum_{i=0}^{\frac{n}{2}-1}a_{i+\frac{n}{2}})\omega_n^{ki} \nonumber$$

这样似乎还是要对每个点求一次单位根，是 $\mathcal O(n^2)$ 的，但是不要忘记单位根的性质

$$(\omega_n^{k})^2=(\omega_{n/2}^{k})$$

对于所有偶数的 $k$，都写成 $\omega_{n}^{2p}$ 的形式，也就是 $\omega_{n/2}^{p}$，这也就是说，我们把奇数的位置全部乘上 $\omega^{1}_{n}$，再把奇数和偶数的部分提取出来，分别递归进行 DIF，那么在第二层乘上 $\omega^{1}_{n/2}$ 实际上就是在第一层乘上了 $\omega^{2}_n$。考虑幂次上的二进制拆分，所以这个是对的。

这里的做法其实是考虑每一个系数会乘上哪些单位根，而 DIT-FFT 实际上是考虑每一个单位根会乘上哪些系数。

最后实际上把所有 $F(\omega_n^{k})$ 按 $k$ 蝴蝶变换了一遍，所以就是输入一个系数向量，输出一个蝴蝶变换后的点值向量

我们有一份非常暴力的实现：

std::vector<std::complex<double>> dif_fft(std::vector<std::complex<double>>& x) {
    int N = x.size();

    if (N == 1) {
        return x;
    }

    std::vector<std::complex<double>> even(N / 2);
    std::vector<std::complex<double>> odd(N / 2);

    for (int i = 0; i < N / 2; i++) {
        even[i] = x[i] + x[i + N / 2];
        odd[i] = (x[i] - x[i + N / 2]) * std::polar(1.0, -2 * M_PI * i / N);
    }

    std::vector<std::complex<double>> evenResult = dif_fft(even);
    std::vector<std::complex<double>> oddResult = dif_fft(odd);

    std::vector<std::complex<double>> result(N);

    for (int k = 0; k < N / 2; k++) {
        result[k] = evenResult[k];
        result[k + N / 2] = oddResult[k];
    }

    return result;
}

巧的是，我们原本的 DIT-FFT 是输入一个经过蝴蝶变换后的系数向量，输出一个点值向量，而 DIF-FFT 是输入一个系数向量，输出一个蝴蝶变换后的点值向量。

那我们直接先 DIF-FFT 得到蝴蝶变换后的点值向量，再 DIT-FFT 翻转回来不就能得到系数向量了吗？

直接按这样实现可以再卡大概 $70\text{ms}$。

再优化

DIT-FFT因为从小到大，每层都要重新处理单位根，单位根乘法是 $O(n\log n)$ 次的。

DIF-FFT因为从大到小，但是每层计算的时候都要即时贡献，单位根乘法也是 $O(n\log n)$ 次的。

那如果我们直接对不蝴蝶变换的系数向量做 DIT-FFT 呢？

我们仍然会得到一个点值的数组，而其正是蝴蝶变换后的数组，只要我们对中途用到的原根也蝴蝶变换一下就行了。

更具体的，我们可以在 DIF-FFT 的过程中做 DIT-FFT，也就是说，我们除了最外层大循环以外都是 DIT-FFT 的操作，对 DIT-FFT 也可以像这样直接反过来。这样我们的原根移动次数可以优化到 $O(n)$ 级别的。

对于预处理原根的方法，我们也可以改变一下，以 $\bmod 998244353$ 举例，我们考虑每次用到的原根都是 $3^{\frac{p-1}{n}}$，而 $n$ 是 $2$ 的幂，把 $p$ 拆成 $7\times 17\times 2^{23}=119\times 2^{23}$ 的形式，我们把原来的底数从 $3$ 换成 $3^{119}$，这样我们只要维护底数的各个幂即可。

至于如何直接预处理蝴蝶变换后的原根，先直接预处理出 $g^{2^k}$ 放在 $2^{21-k}$ 处，也就是蝴蝶变换后的结果，为什么是 $21-k$ 次方是因为 $\frac{p-1}{n}$ 对应的就是它。

其次 $g^{2^j+2^k}=g^{2^j}\times g^{2^k}$，每次拿两个位拼起来就行了

#include <algorithm>
#include <vector>
#include <cctype>
#include <cmath>
#include <cstring>
#include <iostream>

typedef long long ll;
using namespace std;
const ll g = 3, gi = 332748118, mod = 998244353;
// 3^119
const ll prebase = 15311432;
const int N = 2e6 + 1e5 + 10;

ll f_pow(ll a, ll k) {
	ll base = 1;
	for (; k; k >>= 1, a = a * a % mod)
		if (k & 1)
			base = base * a % mod;
	return base;
}

namespace NTT {
	ll w2[N];
	int n;
	void init(int n = N) {
		int t = min((n > 1 ? __lg(n) - 1 : 0), 21);
		// 直接预处理蝴蝶变换后的单位根
		w2[0] = 1, w2[1 << t] = f_pow(prebase, 1 << (21 - t));
		// 翻转后的单位根, 大的对应小的
		for (int i = t; i; i--)
			w2[1 << (i - 1)] = w2[1 << i] * w2[1 << i] % mod;
        
		// 除去最后一个 1 与只留最后一个 1, 这个时候本身就是已经倒序的, 自然这样处理出来的也是倒序的
		for (int i = 1; i < (1 << t); i++)
			w2[i] = w2[i & (i - 1)] * w2[i & -i] % mod;
	}

	inline void NTT_init(int len) {
		n = 1 << len;
	}

	void DIF(vector<ll> &a) {
        // 外层循环是 DIT
		for (int i = n >> 1; i >= 1; i >>= 1) {
			for (int j = 0, og = 0; j < n; j += (i << 1), og++) {
				for (int k = 0; k < i; k++) {
					ll x = a[j + k], y = a[i + j + k] * w2[og] % mod;
					a[i + j + k] = (x - y + mod) % mod;
					a[j + k] = (x + y) % mod;
				}
			}
		}
	}

	void DIT(vector<ll> &a) {
        // 外层循环是 DIF
		for (int i = 1; i < n; i <<= 1) {
			for (int j = 0, og = 0; j < n; j += (i << 1), og++)
				for (int k = 0; k < i; k++) {
					ll y = (a[j + k] + a[i + j + k]) % mod;
					a[i + j + k] = (a[j + k] - a[i + j + k] + mod) * w2[og] % mod;
					a[j + k] = y;
				}
		}
	}
	inline void DNTT(vector<ll> &a) {
		DIF(a);
	}
	inline void IDNTT(vector<ll> &a) {
		DIT(a);
		reverse(a.begin() + 1, a.begin() + n);
		ll inv = f_pow(n, mod - 2);
		for (int i = 0; i < n; i++)
			a[i] = a[i] * inv % mod;
	}
}

int n, m;
vector<ll> a, b;
int main() {
	scanf("%d%d", &n, &m);
	a.resize(n + m + 1, 0);
	b.resize(n + m + 1, 0);
	for (int i = 0; i <= n; i++)
		scanf("%lld", &a[i]);
	for (int i = 0; i <= m; i++)
		scanf("%lld", &b[i]);
	int k = std::max((int)ceil(log2(n + m + 1)), 1);
	NTT::init();
	NTT::NTT_init(k);
	a.resize(1 << k);
	b.resize(1 << k);
	fill(a.begin() + n + 1, a.begin() + (1 << k), 0);
	fill(b.begin() + m + 1, b.begin() + (1 << k), 0);
	NTT::DNTT(a);
	NTT::DNTT(b);
	for (int i = 0; i < (1 << k); i++)
		a[i] = a[i] * b[i] % mod;
	NTT::IDNTT(a);
	for (int i = 0; i < n + m + 1; i++)
		printf("%lld ", a[i]);
	puts("");
	return 0;
}

听说还能再快点 最新最热多项式乘法常数优化 - Kevin090228 的博客 但是摆了。

多项式基础运算

半在线卷积

Link

给定 $g_{0\ldots n-1}$，规定 $f_0=1$，求 $f_{0\ldots n-1}$ 满足

$$f_i=\sum_{j=1}^{i}f_{i-j}g_{j}$$

计算 $f_i$ 需要用第 $i$ 项之前的值。考虑分治，先算出前半部分的值。那么每次我们令

$$f_i\leftarrow f_i+\sum_{j=l}^{mid}f_{j}g_{i-j}$$

即可。

不难发现每次会用到的都是 $g$ 的一段前缀的 DFT 结果，所以我们可以预处理出来。对每个 $n=2^k$ 求出这一段前缀的 DFT 结果，具体实现可以看代码。

// [l, r)
void CDQ(Poly &A, Poly &s1, int l, int r, const Poly &s2) {
	if (l + 1 == r) {
		return ;
	}
	int mid = l + r >> 1;
	int n = r - l;
	CDQ(A, s1, l, mid, s2);
    // 将前半放到 s1 里面去, s1 后半部分清零
	std::copy(A.begin() + l, A.begin() + mid, s1.begin());
	std::fill(s1.begin() + (n >> 1), s1.begin() + n, 0);
    // NTT
	NTT::DNTT(s1, n);
    // 乘上去
	for (int i = 0; i < n; i++)
		s1[i] = 1ll * s1[i] * s2[i + n] % mod;
	NTT::IDNTT(s1, n);
    // 对后半部分贡献
	for (int i = n / 2; i < n; i++)
		A[i + l] = Plus(A[i + l], s1[i]);
	CDQ(A, s1, mid, r, s2);
}

void SemiConv(Poly &A, Poly &B) {
	static Poly s1, s2;

	int m = B.size();
	int k = std::ceil(std::log2(m)) + 1;
	A.resize(1 << k, 0);
	B.resize(1 << k, 0);
	s1.resize(1 << k), s2.resize(1 << k);

	A[0] = 1;
	int n;
	// 对 G 预处理 DFT 结果, 保存在 s2 当中
	for (n = 1; (n >> 1) < m; n <<= 1) {
		std::copy(B.begin(), B.begin() + n, s1.begin());
		NTT::DNTT(s1, n);
		std::copy(s1.begin(), s1.begin() + n, s2.begin() + n);
	}
	CDQ(A, s1, 0, n >> 1, s2);
}

多项式 exp

设 $B(x)\equiv \mathrm e^{A(x)}\pmod {x^n}$，给定 $A(x)$，求 $B(x)$

考虑对这个式子左右两边求导。

$$B'(x)\equiv \mathrm e^{A(x)}A'(x)$$

展开。

$$\begin{aligned} B'(x)&\equiv B(x)A'(x)\\ \sum_{i=0}^{n-1}(i+1)b_{i+1}x^i&\equiv\Big(\sum_{i=0}^{n-1}b_ix^i\Big)\Big(\sum_{i=0}^{n-1}(i+1)a_{i+1}x^i\Big) \end{aligned}$$

考虑前者的第 $k$ 项系数，有：

$$\begin{aligned} (k+1)b_{k+1}&\equiv \sum_{i+j=k}(j+1)b_ia_{j+1}\\ b_{k+1}&\equiv \frac{1}{k+1}\sum_{i=0}^{k}(i+1)a_{i+1}b_{k-i}\\ b_{k}&\equiv \frac{1}{k}\sum_{i=1}^{k}ia_ib_{k-i} \end{aligned}$$

这个形式就是我们熟悉的半在线卷积的形式，这个 $\frac{1}{k}$ 可以在分治到底部的时候乘上。

多项式 ln

设 $B(x)\equiv \mathrm \ln{A(x)}\pmod {x^n}$，给定 $A(x)$，求 $B(x)$

仍然考虑对这个式子两边求导。

$$B'(x)\equiv \frac{A'(x)}{A(x)}$$

到这个地方就可以用多项式乘法逆解决了，但是还可以再推一推。

$$\begin{aligned} A'(x)&\equiv A(x)B'(x)\\ \sum_{i=0}^{n-1}(i+1)a_{i+1}x^i&\equiv \Big(\sum_{i=0}^{n-1}a_ix^i\Big)\Big(\sum_{i=0}^{n-1}(i+1)b_{i+1}x^i\Big)\\ \end{aligned}$$

提出第 $k$ 项系数。

$$\begin{aligned} (k+1)a_{k+1}&\equiv \sum_{i+j=k}a_{i}(j+1)b_{j+1}\\ (k+1)a_{k+1}&\equiv \sum_{i=0}^{k}(i+1)a_{k-i}b_{i+1}\\ (k+1)a_0b_{k+1}&\equiv (k+1)a_{k+1}-\sum_{i=0}^{k-1}(i+1)a_{k-i}b_{i+1}\\ (k+1)a_0b_{k+1}&\equiv (k+1)a_{k+1}-\sum_{i=1}^{k}ia_{k-i+1}b_{i} \end{aligned}$$

因为 $a_0=1$，令 $k=k-1$，所以

$$kb_k\equiv ka_k-\sum_{i=1}^{k}(k-i)a_{i}b_{k-i}$$

半在线卷积就可以得到 $kb_k$。