几何解释
ALG 不等式指的是,当 a,b∈R 且 0<a<b 时有如下不等式成立:
ab<lnb−lnab−a<2a+b
即几何平均值小于对数平均值,对数平均值小于算数平均值。
我们先证明右半侧,这与 lnb−lna>(b−a)⋅a+b2 等价。
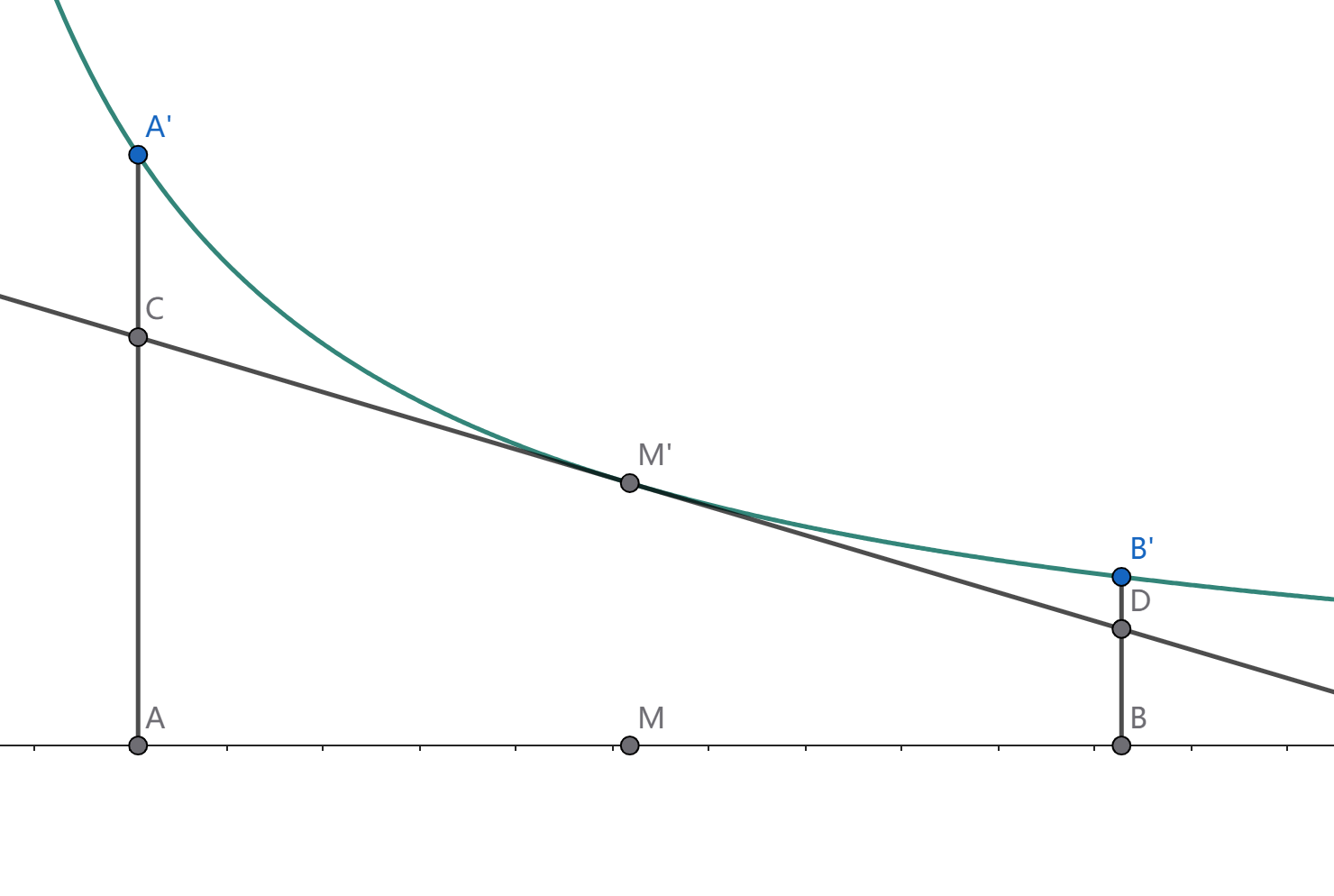
建立平面直角坐标系 xOy,设 A=(a,0),A′=(a,a1),B=(b,0),B′=(b,b1),M=(2a+b,0),M′=(2a+b,a+b2)。
显然直线 AA′,BB′,MM′ 均垂直于 x 轴,A′,B′,M′ 均位于函数 f(x)=x1 图像上,过点 M′ 作关于函数 f(x)=x1 图像的切线 ℓ,分别交直线 AA′,BB′ 于 C,D。
显然有曲边梯形 AA′B′B 的面积大于梯形 ACDB 的面积,即 lnb−lna=∫abx1dx>(b−a)⋅a+b2。
然后证明左半侧:先 a=ep,b=eq,原式变为 e2p+q<q−peq−ep,等价于 eq−ep>(q−p)⋅e2p+q
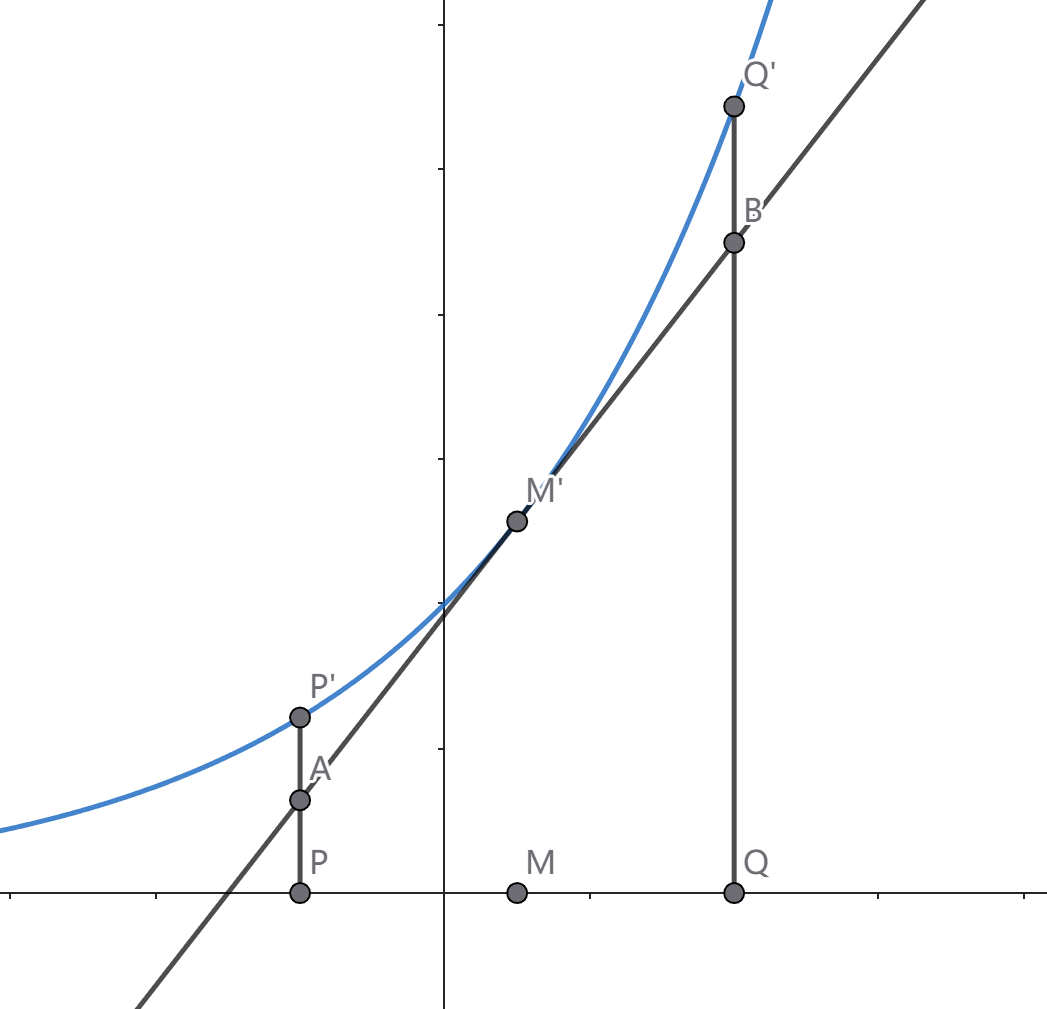
设点 P=(p,0),P′=(p,ep),Q=(q,0),Q′=(q,eq),M=(2p+q,0),M′=(2p+q,e2p+q)。
显然直线 PP′,QQ′,MM′ 均垂直于 x 轴,P′,Q′,M′ 均位于函数 f(x)=ex 图像上,过点 M′ 作关于函数 f(x)=ex 图像的切线 ℓ,分别交直线 PP′,QQ′ 于 A,B。
显然曲边梯形 PP′Q′Q 的面积大于梯形 PABQ 的面积。即 eq−ep=∫pqexdx>(q−p)⋅e2p+q。
注意这一侧的不等式证明中 A 可能会在 x 轴下方,把我们上面的所说的面积定义改为有向面积即可(一,二象限面积减去三,四象限面积,显然仍有不等号成立),也就是梯形面积的定义为 ∫pqg(x)dx,其中 g(x) 的图像是直线 ℓ。
这种证法虽然简洁明快,但是没法写在考卷上,因为我们难以在短暂的篇幅内仅使用高中的知识证明曲线 y=x1 和 y=ex 的下方面积,而且光是设点就需要很长的篇幅。所以什么时候把一元微积分下放到高考啊?
考场写法
很喜欢一句话:

也即,我们要说明 f(x)>g(x),其中 x>0 的一个充分条件是:f(0)≥g(0) 且恒有 f′(x)>g′(x)。
所以我们将证明改写为如下形式:
-
lnb−lnab−a<2a+b
即证 lnb−lna>(b−a)⋅a+b2,换元令 a=m−t,b=m+t,其中 t∈(0,m)。
只需证 ln(m+t)−ln(m−t)>m2t,令 f(t)=ln(m+t)−ln(m−t)−m2t。
f′(t)=m+t1+m−t1−m2=m2−t22m−m22m>0。故 f(t) 单调增,f(t)>f(0)=0,证毕。
-
ab<lnb−lnab−a
令 a=ep,b=eq,即 (q−p)⋅e2p+q<eq−ep,换元令 p=m−t,q=m+t,其中 t>0。
只需证 2t⋅em<em+t−em−t,令 f(t)=2t⋅em−em+t+em−t。
f′(t)=2em−(em+t+em−t),f′′(t)=−(em+t−em−t)<0
故 f′(t)<f′(0)=0⟹f(t)<f(0)=0,证毕。


