2025 新高考 I 卷数学 P19(3) 的一个几何解法

碎碎念：折腾了一个下午发现 MathJax 在 Hexo 上简直就是不能用，渲染到处出错，还不如改回 KaTeX，反正现在还是一个不支持加包也不支持 \newcommand 的状态，所以说 Hexo 不好用呢，以后长文章都会丢到 mkdocs 的那个博客上了。

令 $f(x)=5\cos (x)-\cos (5x+t)$，求：

$$\min_{t\in \mathbb R}\left\{\max_{x\in \mathbb R}f(x)\right\}$$

先求导，有：

$$f'(x)=5\sin(5x+t)-5\sin (x)=10\left(\cos\left(\frac{6x+t}{2}\right)\sin\left(\frac{4x+t}{2}\right)\right)$$

令 $f'(x)=0$，$x$ 的取值集合为：

$$\left\{x:\frac{6x+t}{2}=\frac{\pi}{2}+k\pi\right\} \cup \left\{x:\frac{4x+t}{2}=k\pi\right\}$$

所以极值点有 $x=\dfrac{(2k+1)\pi -t}{6}$ 或 $x=\dfrac{2k\pi-t}{4}$。

先考虑当 $x=\dfrac{(2k+1)\pi-t}{6}$ 的情况，设：

$$\begin{aligned} g(k)&=5\cos\left(\frac{(2k+1)\pi-t}{6}\right)-\cos\left(\frac{(10k+5)\pi -5t}{6}+t\right)\\ &=5\cos\left(\frac{(2k+1)\pi-t}{6}\right)-\cos\left(\frac{(10k+5)\pi +t}{6}\right) \end{aligned}$$

其中 $k\in \mathbb Z$，令 $\alpha =\dfrac{(2k+1)\pi-t}{6},\beta =\dfrac{(10k+5)\pi +t}{6}$，显然有 $\alpha +\beta =(2k+1)\pi$，$g(k)=5\cos (\alpha)-\cos((2k+1)\pi -\alpha)=6\cos (\alpha)$，显然只需考虑 $k=0,1,2,3,4,5$ 的情形，因为 $g(k)=g(k\bmod 6)$，即：$\displaystyle \max_{k=0}^{5}g(k)=\max_{x\in \mathbb Z}g(k)$。

不难注意到，当 $t=0$ 时，$k=0,1,2,3,4,5$ 对应的 $\alpha$ 分别是 $\dfrac{\pi}{6},\dfrac{3\pi}{6},\dfrac{5\pi}{6},\dfrac{7\pi}{6},\dfrac{9\pi}{6},\dfrac{11\pi}{6}$，在平面直角坐标系上画出与 $x$ 轴正半轴夹角为某个 $\alpha$ 的所有单位向量，有：

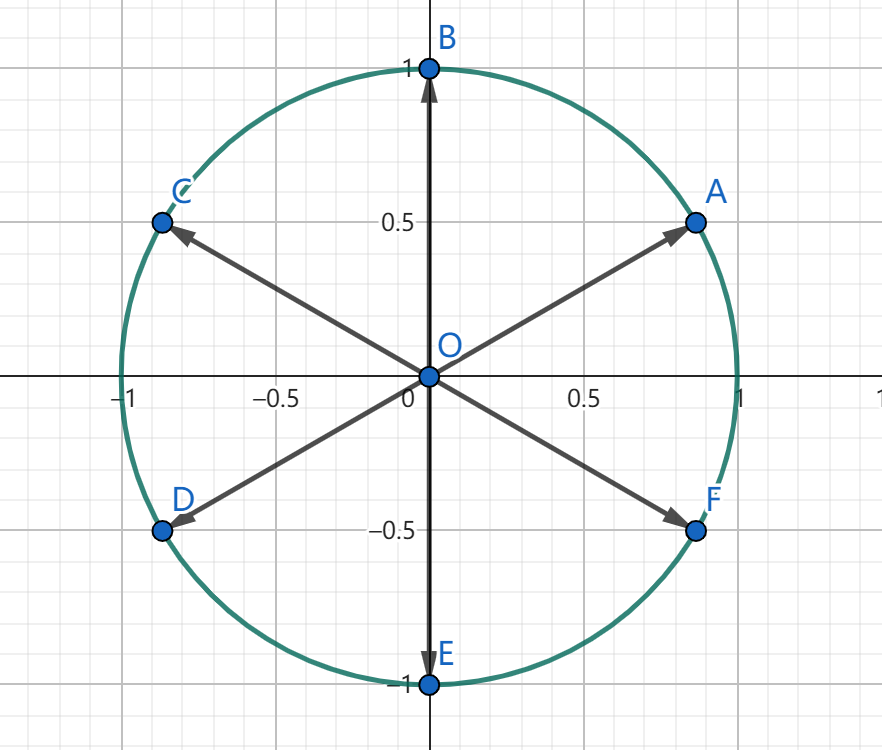
此时，有 $\max g(k)=6\cos \dfrac{\pi}{6}=3\sqrt 3$。对于 $t\neq 0$ 的情况，这相当于将这 $6$ 条向量同时顺时针旋转 $\dfrac{t}{6}$，显然，无论如何，至少有一条向量与 $x$ 轴正半轴夹角的绝对值 $\le \dfrac{\pi}{6}$，即对应 $\alpha$ 有 $\cos \alpha \ge 3\sqrt 3$。

也即，无论 $t$ 如何取，总有 $\displaystyle\max_{k\in \mathbb Z} \left\{f\left(\dfrac{(2k+1)\pi -t}{6}\right)\right\}\ge 3\sqrt 3$，等号取到当且仅当 $t=2a\pi,a\in \mathbb Z$。

再来讨论当 $x=\dfrac{2k\pi-t}{4}$ 时的情况：

$$h(k)=5\cos\left(\frac{2k\pi-t}{4}\right)-\cos\left(\frac{10k\pi -5t}{4}+t\right)=4\cos\left(\frac{2k\pi -t}{4}\right)$$

不难得到 $h(k)\le 4<3\sqrt 3$，显然，无论对于何种 $t$，$f(x)$ 的最大值都不会在这种情况下产生。

综上，我们断言：无论对于何种 $t$，总有 $f(x)\ge 3\sqrt 3$，等号成立当且仅当 $t=2k\pi ,k\in \mathbb Z$。故答案即为 $3\sqrt 3$。